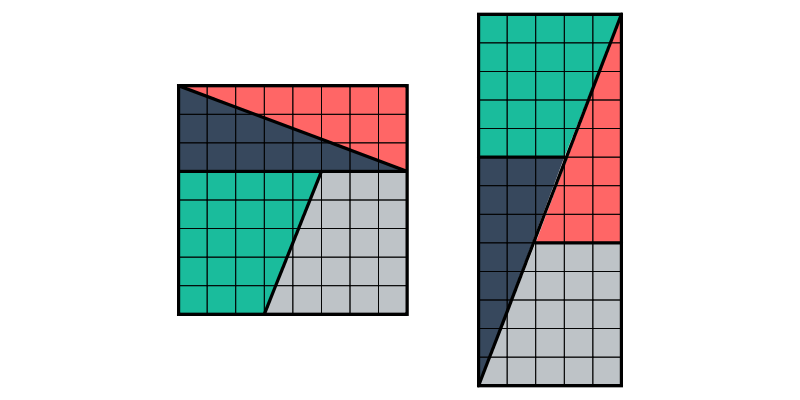
A favorite puzzle/paradox of Lewis Carroll based on Fibonacci numbers. The two figures are “obviously” composed of the same pieces, yet they have different areas!

Author: Brent Yorgey

Download raw source code

> {-# LANGUAGE NoMonomorphismRestriction #-}
> import Diagrams.Prelude

The standard infinite list of Fibonacci numbers.

> fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
> 
> thick = 0.15

Create a grid by gluing together a bunch of squares.

> grid x y = frame <> lattice
>   where s       = unitSquare # lw 0.02 # freeze
>         frame   = rect (fromIntegral x) (fromIntegral y)
>                 # lw thick # freeze
>         lattice = centerXY . vcat . map hcat . replicate y . replicate x $ s

The trapezoid and triangle shapes, with sides lengths based on two Fibonacci numbers.

> trap s1 s2 = lw 0 . strokeT . close
>            . fromOffsets . map r2 $ [(0,-s2), (s2,0), (0,s1)]
> tri s1 s2  = lw 0 .  strokeT . close
>            . fromOffsets . map r2 $ [(s1,0), (0,s1+s2)]

Draw the paradox diagram based on the nth Fibonacci number.

> paradox n drawDiags = (sq ||| strutX s2 ||| rect) # centerXY
>   where f1 = fibs !! n
>         f2 = fibs !! (n+1)
>         s1 = fromIntegral f1
>         s2 = fromIntegral f2
> 
>         trap1 = trap s1 s2 # fc yellow
>         trap2 = trap s1 s2 # fc green
>                            # rotateBy (1/2)
> 
>         tri1  = tri s1 s2  # fc red
>         tri2  = tri s1 s2  # fc blue

The four shapes assembled into a square.

>         sq = (if drawDiags then sqDiags else mempty)
>              <> grid (f1+f2) (f1+f2)
>              <> sqShapes
>         sqDiags = (fromVertices [p2 (0,s2), p2 (s2,s1)] <>
>                    fromVertices [p2 (s2,0), p2 (s2,s1+s2)] <>
>                    fromVertices [p2 (s2,0), p2 (s1+s2,s1+s2)])
>                 # stroke
>                 # lw thick
>                 # freeze
>                 # centerXY
> 
>         sqShapes = (traps # centerY ||| tris # centerY)
>                  # centerXY
>         traps = trap2 # alignL
>                       # translateY (s1 - s2)
>              <> trap1
>         tris  = tri1 # alignBL
>              <> tri2 # rotateBy (1/2)
>                      # alignBL

The four shapes assembled into a rectangle.

>         rect = (if drawDiags then rDiags else mempty)
>                <> grid (2*f2 + f1) f2
>                <> rShapes
> 
>         rShapes = (bot # alignTL <> top # alignTL) # centerXY
>         bot = trap1 # alignB ||| rotateBy (-1/4) tri1 # alignB
>         top = rotateBy (1/4) tri2 # alignT ||| trap2 # alignT
> 
>         rDiags = (fromVertices [p2 (0,s2), p2 (2*s2+s1, 0)] <>
>                   fromVertices [p2 (s2,0), p2 (s2,s1)] <>
>                   fromVertices [p2 (s1+s2,s2-s1), p2 (s1+s2,s2)]
>                   )
>                  # stroke
>                  # lw thick
>                  # lineCap LineCapRound
>                  # freeze
>                  # centerXY

Draw the order-4 diagram with thick lines in the middle. Passing the argument False causes the thick lines to be omitted, revealing the skinny gap in the rectangular assembly. Lower-order diagrams make the gap more obvious; higher-order diagrams make it increasingly less obvious (but make the grid smaller).

> example = pad 1.1 $ paradox 4 True